サカトマのゲーム設計ノート
三角比とその応用
RPGで,ある特定の場所を探したいときってありますよね?
目的地だとか,宝箱だとか,いろいろ……
図Aのように,その位置が,現在地からどの方角にあるのか,知りたいですよね.
その方角を知らせてくれるアイテムを作ってみましょう!

図A.目的地の方角を示すアイテムの使用例
角度を扱ううえで欠かせない,数学の道具があります.
それは,三角比です.
こういうのを聞くと「あぁ……数学を見るとじんましんが出るんじゃ」と悲鳴が聞こえてきそうですが,
安心してください.中学生の知識を前提に丁寧に教えます.
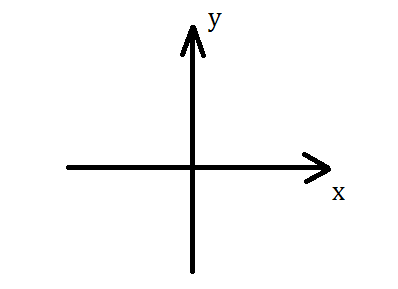
図B.二次元座標平面
はい,さすがに図Bは見覚えがあってほしいです.
横がx軸で,縦がy軸です.この平面上に点を打つと,それに対応する(x, y)の組が一意に定まります.
逆に,(x, y)の組を与えると,それに対応する点も,平面上に一意に打つことができます.
このとき,(x, y)を点の座標といいます.
ここでは,x軸とy軸の交点を原点といって,
その座標を(0, 0)とします.
右に行くほどxは大きくなり,上に行くほどyは大きくなります.
このページの図では,ね.
ゲームのみならず,マシンの画面では,下に行くほどyが大きくなります.
初心者はここを忘れがちなので注意!
また,マシンの画面では,画面の一番左上が原点となる
ことにも注意しよう.
このページではとりあえず,「上に行くほどyが大きくなる」とします.
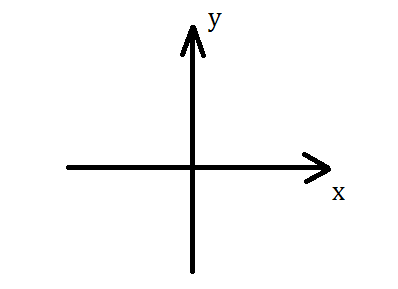
図B.二次元座標平面
話を元に戻しましょう.
座標平面上の原点を中心に,半径1の円を描いてみましょう(図C).
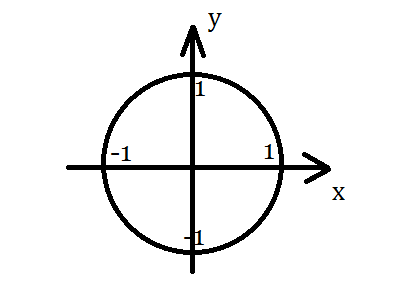
図C.単位円
この半径1の円を,よく単位円といいます.
で,原点から1本,半直線を引いてみます(図D).
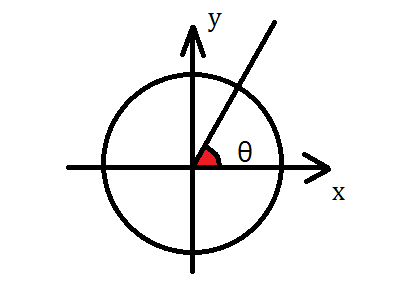
図D.単位円と半直線
さて,問題です.単位円と直線の交点の座標(図Eの「?」)は,どのように求まるでしょうか?
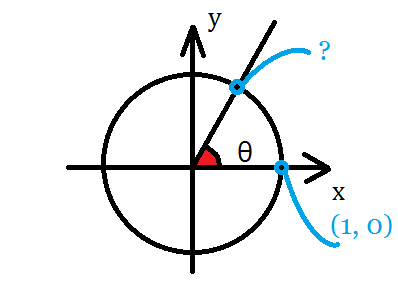
図E.座標は何だ?
直線の特徴を示すものといえば,角度θでしょうね.
このθをx軸と直線がなす角とかいって,x軸から反時計回りに進む方向が正となります.
ちなみに,θは180度を超えてしまっても構いません.
さてθが決まれば,座標も一つに決まるはずです.
とはいえ,困りましたね……
θだけでは,中学生の持てる技で,座標を求めるのには無理があります.
そこで,この座標を(cosθ, sinθ)としてしまうわけです.
数学ではそういう決まりごとになっているんです.
これが,三角比の定義なんです.
ついでに,sinθをcosθで割ったものをtanθとしちゃおう,というわけです.
この値は,直線の「傾き」と同じです.
高校1年では直角三角形から定義していくのですが,2年生で結局この定義になるんです.
実は,この定義を問うた入試を出した大学があります.
東京大学っていうんですけれどね.
定義は導入問題で,真の問題は「角の加法定理を証明せよ」というものでして,
この定理を証明するためには,
直角三角形から定義するよりも座標から定義したほうが理解しやすい,
ということです.
いかなる定理も,定義が必要なんです.
数学を学ぶなら,定義をしっかり押さえましょう.
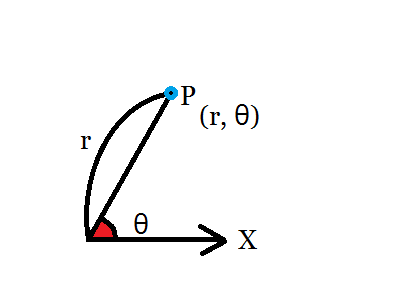
図F.極座標
図Fのように,y軸がなくとも,
原点からの距離,軸となす角の2つを指定するだけで点を定めることができます.
このシステムを「極座標」といいます.
今までの座標のシステムよりも,極座標の方が便利な場面もあります.
たとえば洗面所の蛇口.横に回すと温度を調節できて,縦に動かすと流量を調節できますね.
あれは極座標スタイルですよねー.

図A.目的地の方角を示すアイテムの使用例
ではいよいよ,このアイテムを実装しましょう〜.
ここからは,実装するという意味で,
座標の取り方はマシンの画面に沿うことにします.
つまり,マシンの画面では,下に行くほどyが大きくなります.
これに伴って,なす角θは時計回りに進む方向が正になります.
たとえば,図Gのような状況だとします.

図G.位置関係の例
もしも目的地が現在地の真右にあるのなら,矢印の指すべき角度は0度です.
つまり,矢印画像は右向きがよいでしょう.
まず,現在地と目的地のx, y座標の差を求めます.
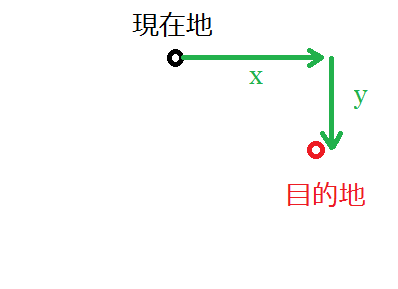
図H.座標の差を求める
こうすることで,この2点を結んだ直線の「傾き」を求めることができます.
これで,tanθ=「傾き」となるθが存在するはずで
これが矢印を回転させる角度となります!
これは,計算機に任せましょう!(ウディタなら「変数操作」,C++なら数学ライブラリで求められるはず)

図I.回転角度を求める
お疲れ様でした.
1.(sinθ)^2 + (cosθ)^2 = 1 を証明しなさい.
(ヒント:三平方の定理)
広告