サカトマの計算理論ノート
パソコンでも解けない計算問題
厳密な定義は難しすぎるので，「わかったような気になれる解説」になります．
直感のお話なので，もし詳しく知りたくなったらいろいろな資料を読んでみるといいかもしれません．
あくまで，「P vs NP ? なんだそれ」という人向けになります．
世の中には「パソコンで計算しても絶望的な時間を要する（とされている）問題」が存在します．
たとえば，次のような問題があります．
【例】巡回セールスマン問題
あなたはセールスマンとして，各家々を訪問することになりました．
事務所を出発点として家A, B, C, D, Eをすべて訪問し，再び事務所に戻らなければなりません．
家や事務所の間を移動するのにかかる時間は，次の表のとおりです．
| A | B | C | D | E |
| 事務所 | 14分 | 4分 | 12分 | 5分 | 15分 |
| A | | 10分 | 5分 | 7分 | 20分 |
| B | | | 8分 | 10分 | 12分 |
| C | | | | 4分 | 20分 |
| D | | | | | 18分 |
このとき，あなたはどのような経路をとれば，最も早く事務所に戻れるでしょうか．
もちろん全部の経路を試して，それぞれにかかる時間を計算し
時間最小の経路を出せばよいのですが，その経路の数はいくつあるでしょう？
まず一番目にどの家に行くか，これは5通りあります．
さらに，二番目にどの家に行くか，一番目の家を除いた4通りあります．
さらにさらに，三番目にどの家に行くか，既に訪問した家を除いた3通りあります．
このように考えると，5x4x3x2x1=120通りも存在します．
ちなみに，1x2x ... x n の値のことを「nの階乗」といって，n!と表します．
ただ，これはもう少し効率よくできます．
ひとつの経路に対して，それを逆順に訪問する経路をたどったとき
元の経路と同じ時間だけかかります．
つまり，逆順に訪問するパターンは考えなくてもいいのです．
だから，調べるべき訪問順は，半分の60通りだけです．
これは，本当に効率がよくなっているのでしょうか？
60通りくらいなら，パソコンで素早く解けそうですが，
訪問する家が1件増えて6件になったらどうでしょう．
経路の数は，6倍になります．
さらに家が1件増えて7件になったら，5件のときに比べて経路の数は6x7=42倍になります．
ちなみに，20件では2400000000000000000(0が18個)通り以上の数になります．
このように，掛け算すると経路の数は爆発的に増加します．
この現象を専門用語で「組合せ爆発」といったりします．
組合せ爆発はとてもバカにできません．
9999と10000は誤差レベルだと思われがちですが，
その計算コストの差は実に10000倍になるのです．
さっきの工夫では経路の数を半分に減らせましたが，
1件増えるだけで，その工夫の効果が笑ってしまうほど薄くなってしまいます．
この「巡回セールスマン問題」はNP困難という種類に分類され，
効率よく解く方法が世界中で研究されています．
そして，いまだにその方法は見つかっていません．
「効率よく」って具体的にはどういうことでしょうか．
そのためには，「多項式時間」という概念が重要になります．
考える問題に現れるデータの数をサイズといいます．
たとえば，巡回セールスマン問題で訪ねる家の件数がサイズになります．
問題Aのサイズをnとします．
このとき，問題Aがnの多項式時間で解けるといったら，
解くために必要な時間が，長くてもcn^a以下になる定数c, aが存在する(n^aはnのa乗)
ことをいいます．「必要な時間」というのはつまり，関数（ウディタで言うコモンイベント）のコマンド数に比例すると思ってください．
指数にある a が小さいほど速く解けることになります．
たとえば、「線の一筆書き」を例にとってみましょう．
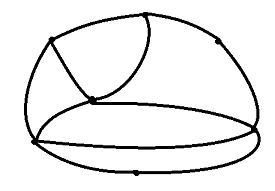この図にある，すべての線を一度ずつ通る道筋は存在するでしょうか？
数学界で有名なオイラーは，次のようなルールを見つけました．
道の交差点につながっている線の本数[次数]を数える．
その本数が奇数となるような交差点が0個か2個であれば，一筆書きができる．
さもなくば，一筆書きはできない．
ということで，次数が奇数となる交差点の数を数え上げて
0個か2個であれば一筆書きはできる，そうでなければできない，と判断できます．
（図の場合は，次数が奇数の交差点が2つだけなので，一筆書きできます）
この判定は，交差点の数をnとし，アルゴリズムを工夫すれば n^2（の定数倍）の時間でできます．
つまり，線の一筆書き問題は多項式時間で解けます．
「効率のいい方法」というのは，多項式時間で解ける方法だったのです．
クラスPとは多項式時間で解ける○×クイズの集まり．
線の一筆書き問題は，「一筆書きできる、○か×か」という問題ですね．
多項式時間で解けるので，線の一筆書き問題はクラスPに属します．
多項式時間で解けても，○×以外が答えとなる問題はクラスPに含まれません．◯か×か（YesかNoか）で答える問題に絞っています．
たとえば、「32+34=?」という問題はクラスPには含まれません．
もう一つ，問題の例を出しましょう．
上で出したのは「線の一筆書き」ですが，今度は「点の一筆書き」です．
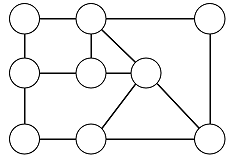
この図で，同じ丸（点）を二度通らずに，すべての点を通る「ループ」はあるでしょうか？
いくら探しても見つからないから，ループはないよ！というのは答えになりません．
探し漏れがある可能性があるからね．まぁ実際にはないんだけど．
これこそ，全通りの道順を探さないと求められないでしょう（今のところは※）．
※断定してしまうと，後述の P vs NP が解けたことになります．
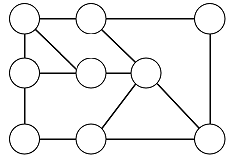
一方でこの図の場合，ループは存在します．
存在性の証明はとても簡単．
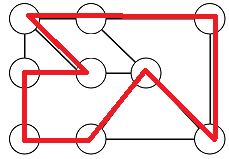
なぜなら，存在する例を示せばいいだけだから．
この赤いループが，同じ点を二度通らずすべての点を通っているということはすぐに（多項式時間で）わかります．
クラスNPとは，「証拠」が与えられたときに
○であることが多項式時間で検証できるような○×クイズの集まり．
クラスco-NPとは，「証拠」が与えられたときに
×であることが多項式時間で検証できるような○×クイズの集まり．
ここらへんからわかりにくいですね．もっと簡単に例えましょう．
○×クイズを多項式時間で解くことができれば，そのクイズはクラスPに属します．
具体例を用いることで，そのクイズの答えが○であることを
多項式時間で確認できることができれば，そのクイズはクラスNPに属します．
点の一筆書きは，証拠（赤いループ）を与えられたときにすぐ正解であることが確認できるので，
クラスNPに属します．
線の一筆書きも，クラスNPに属します．
クラスPに属するクイズは，クラスNPに属します．
問題は，「クラスNPに属するクイズがすべて，クラスPに属するか？」ということです．
これが，P vs NP 問題．解ければ賞金100万ドルが手に入る「ミレニアム懸賞問題」の一つです．
たとえば，「点の一筆書き」はクラスNPに属しますが，
クラスPに属するか，つまり多項式時間で解けるかどうかということはわかっていません．
「点の一筆書き問題」は，NPに属する問題の中で最も難しい（解くのに時間がかかる）とされている部類に属します，
そのような部類の性質をNP完全といいます．
つまり，NP完全とは次の2つを満たす問題Qの性質をいいます．
・QはNPに属する．
・NPに属するどの問題qからも多項式時間で問題Qに変換することができる．
点の一筆書き以外にも，多くの問題がNP完全であることが証明されており，
NP完全である問題は互いに同じくらい難しいという特徴があります．
また，クラスNPの中で最も難しい問題であることから，
NP完全問題のいずれかが多項式時間で解ける方法が見つかれば，P vs NP 問題が解けます．
（NPに属するどの問題qも，NP完全の問題に変換して解けば，qは多項式時間で解くことができる．）
すなわち，「点の一筆書き問題」を多項式時間で解く方法を見つければ，100万ドルが手に入ります．
ではNP完全問題はどのくらい難しいのか？
1より大きい定数cを用いて，c^nの時間で求められます．
cをいかに小さくできるかが世界中で研究されていたりします．
しかしそれでも，多項式よりも大きいのです．
累乗の指数にnが乗っかる数と，多項式の数との間には雲泥の差があるのです．
例えばc=2, n=12のとき，n^2=144に対して2^n=4096と大きく，
この差はnが大きくなるほど爆発的に増加します．
c=1.4 としても，n=200のとき，n^10 はおよそ 10^23ですが，
1.4^n は 1.6x10^29よりも大きい．
このように，指数部分にnが乗っかると，とんでもなく大きく膨れ上がります．
どんなa, b>1をとってきても，nを大きくすればn^aよりもb^nの方が圧倒的に大きいのです．
そんなわけで，指数部分にnが乗っかったら，これは多項式時間で解けていないことになります．
NPに属さない，つまり○×クイズでない問題であるが，NP完全以上に難しい問題をNP困難といいます．
どういうことかというと，NP困難の問題がどれか一つでも多項式時間で解ければ，
NPに属するどの問題も多項式時間で解くことができ，P vs NP を解決できます．
冒頭で紹介した「巡回セールスマン問題」は，NP完全の「点の一筆書き」以上に難しいことが証明されています．
つまり巡回セールスマン問題はNP困難です．これを効率よく（多項式時間で）解く方法はまだ見つかっていないのです．
ということで，話が複雑でしたがどうでしょうか．
世の中には「パソコンで計算しても絶望的な時間を要する（とされている）問題」が存在します．
"（とされている）"が割と重要で，これがなければ P vs NP 問題を「否定的に解決した」ことになるからです．
（PとNPが違うことを証明したことになる．）
クラスPとNPは同じなのか．50年経っても解決されていません．